Knowledge and Skills
The Knowledge and Skills overviews show the specific mathematical content students will learn in each unit of study throughout the year. These documents outline both the substantive knowledge (mathematical facts, concepts, and principles) and the disciplinary skills (mathematical techniques and applications) that students will develop. Each unit is broken down to clearly identify what students need to know and what they should be able to do upon completion. Through the systematic development of both knowledge and skills, students build mathematical fluency, reasoning abilities, and problem-solving capabilities appropriate to their stage of learning.
Select a unit to find out more...
Linear Graphs
| Unit Progress Criteria |
| Knowledge |
Skills |
- Linear graphs represent straight lines on a coordinate grid.
- The equation of a linear graph is in the form
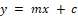 , where m is the slope and c is the y-intercept. , where m is the slope and c is the y-intercept.
- Understanding the slope (gradient) as the rate of change and the y-intercept as the point where the line crosses the y-axis.
|
- Plotting linear equations on a graph by creating a table of values or using the slope and y-intercept.
- Determining the slope and y-intercept from the equation of the line or from a graph.
- Drawing accurate straight lines based on plotted points or using the slope and y-intercept.
- Interpreting the slope and y-intercept from a graph and solving problems involving linear relationships.
|
Proportion
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding proportion as a relationship where two ratios or fractions are equal.
- Knowledge of direct proportion (e.g., if one quantity increases, the other increases in a consistent way) and inverse proportion (e.g., if one quantity increases, the other decreases).
|
- Solving problems involving direct proportion
- Solving problems involving inverse proportion using the relationship between the variables.
- Using proportions to solve real-world problems, such as scaling recipes or determining equivalent ratios.
- Applying cross-multiplication to solve proportion problems and verify the equality of ratios.
|
Standard Form
| Unit Progress Criteria |
| Knowledge |
Skills |
- Standard form (scientific notation) expresses very large or very small numbers in the format: a × 10^n, where a is a number between 1 and 10, and n is an integer.
- Understanding how to convert between standard form and ordinary notation.
|
- Converting numbers from standard form to ordinary notation and vice versa.
- Performing arithmetic operations with numbers in standard form, including addition, subtraction, multiplication, and division.
- Comparing and ordering numbers written in standard form.
- Applying standard form to solve problems involving large or small quantities, such as measurements and scientific data.
|
Sequences
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding sequences as ordered lists of numbers following a specific pattern.
- Knowledge of arithmetic sequences (where the difference between consecutive terms is constant) and geometric sequences (where each term is found by multiplying the previous term by a fixed number).
- Familiarity with the nth term formula for both arithmetic and geometric sequences.
|
- Identifying and continuing arithmetic sequences by adding the common difference.
- Identifying and continuing geometric sequences by multiplying by the common ratio.
- Using the nth term formula to find any term in an arithmetic sequence.
- Solving problems involving sequences, including finding missing terms and describing the pattern.
|
Expanding and Factorising including quadratics
| Unit Progress Criteria |
| Knowledge |
Skills |
- Expanding: Understanding how to use the distributive property to expand expressions, such as multiplying out brackets.
- Factorising: Knowing how to rewrite expressions as products of their factors.
- Quadratic Expressions: Recognising and factorising quadratic expressions of the form x^2 + bx + c.
- Understanding common factor and the difference of squares for factorising.
|
- Expanding expressions like (a + b)(c + d) to a + bc + ad + bd.
- Rewriting expressions such as x^2 + 5x + 6 as (x + 2)(x + 3) by identifying factors.
- Factorising quadratic expressions such as x^2 + 7x + 10 into (x + 2)(x + 5).
- Recognizing and applying factorising techniques for special cases like the difference of squares (e.g., x^2 - 9 = (x - 3)(x + 3)).
- Using factorisation to solve quadratic equations by setting expressions equal to zero and finding roots.
|
Constructions
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding how to use a ruler and compass for basic geometric constructions.
- Knowing how to construct perpendicular bisectors, angle bisectors, and parallel lines.
|
- Accurately drawing lines, angles, and bisecting angles using a ruler and compass.
- Constructing perpendicular bisectors and angle bisectors to find equal angles and midpoints.
- Drawing parallel lines and verifying their properties.
- Applying construction techniques to solve geometric problems and verify properties.
|
Congruence
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding that congruent shapes are identical in shape and size
- Knowing the criteria for congruence in triangles (e.g., SSS, SAS, ASA, RHS).
- Familiarity with the concept of corresponding parts of congruent shapes being equal.
|
- Identifying and proving that shapes or triangles are congruent using congruence criteria.
- Using congruence to solve problems involving matching shapes, angles, and sides.
- Using congruence to justify the similarity or identity of shapes in various geometric contexts.
|
Substitution
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding substitution as the process of replacing variables in an expression or equation with specific values.
- Knowing how to substitute values into algebraic expressions, equations and formulae.
|
- Replacing variables with given values in algebraic expressions and simplifying the result.
- Substituting values into equations and solving for unknown variables.
- Using substitution to evaluate expressions and solve problems in algebra.
|
Solving Equations
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding equations as mathematical statements where two expressions are equal.
- Knowing methods to solve different types of linear equations.
|
- Solving linear equations by isolating the variable on one side of the equation.
- Using algebraic methods such as balancing, combining like terms, and using inverse operations to find the value of the variable.
- Checking solutions by substituting them back into the original equation to verify correctness.
|
Angles in polygons
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding that the sum of interior angles in a polygon depends on the number of sides.
- Knowing the formula for calculating the sum of interior angles: (n - 2) × 180°, where n is the number of sides.
- Familiarity with the formula for each interior angle of a regular polygon: [(n - 2) × 180°] / n.
|
- Calculating the sum of interior angles for any polygon using the formula (n - 2) × 180°.
- Finding each interior angle of a regular polygon by dividing the sum of interior angles by the number of sides.
- Using angle properties to solve problems involving interior and exterior angles of polygons.
- Applying knowledge of angles in polygons to solve geometric problems and proofs.
|
Changing the subject
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding that changing the subject of an equation involves rearranging the equation to solve for a different variable.
- Knowing the rules of algebra to isolate and solve for the desired variable.
- Knowing the inverse operations including squaring and cubing.
|
- Rearranging equations to make a specified variable the subject by using algebraic operations such as addition, subtraction, multiplication, and division.
- Applying inverse operations to isolate the variable of interest.
- Handling complex equations involving multiple variables and ensuring all steps maintain the equation’s balance.
- Checking the new form of the equation by substituting values to verify correctness.
|
Pythagoras
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding Pythagoras' Theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
- Knowing the formula: c^2 = a^2 + b^2, where c is the hypotenuse, and a and b are the other two sides.
- Familiarity with using Pythagoras' Theorem to determine the length of a side in a right-angled triangle.
|
- Applying Pythagoras' Theorem to find the length of the hypotenuse or one of the other sides in a right-angled triangle.
- Solving problems that involve finding missing side lengths in right-angled triangles.
- Using Pythagoras' Theorem to solve real-world problems and geometric proofs.
- Verifying that a triangle is right-angled by checking if the sides satisfy Pythagoras' Theorem.
|
Probability
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding probability as a measure of the likelihood of an event occurring, expressed as a number between 0 and 1.
- Knowing the basic formula for probability: P(A) = Number of favourable outcomes / Total number of outcomes.
- Familiarity with the concepts of experimental probability (based on actual experiments) and theoretical probability (based on possible outcomes).
|
- Calculating the probability of single events by identifying the number of favourable outcomes and the total number of possible outcomes.
- Determining the probability of multiple events, including complementary events (e.g., P(not A) = 1 - P(A)).
- Using probability to solve problems involving simple events, such as rolling dice, drawing cards, or flipping coins.
- Representing probabilities using fractions, decimals, and percentages, and interpreting probability results in various contexts
|
Scatter Graphs
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding scatter graphs as a tool to display and analyse the relationship between two variables.
- Knowing that each point on a scatter graph represents a pair of values.
|
- Plotting data points on a scatter graph based on pairs of values.
- Interpreting the pattern of data points to identify relationships, such as positive correlation, negative correlation, or no correlation.
- Drawing a line of best fit to summarise the overall trend of the data.
- Using the scatter graph and line of best fit to make predictions or draw conclusions based on the data.
|
Inequalities
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding inequalities as mathematical expressions that show the relationship between quantities that are not necessarily equal.
- Knowing the symbols for inequalities: < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to).
|
- Solving linear inequalities by isolating the variable and applying the correct inequality symbol.
- Representing solutions of inequalities on a number line or using interval notation.
- Applying inequalities to solve real-world problems and interpret solutions in context.
|
Averages
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding averages as measures of central tendency: mean, median, and mode.
- Understand how to find the range from a set of data.
- Knowing how to calculate each type of average and understanding their applications.
|
- Calculating the mean by summing values and dividing by the number of values.
- Finding the median by ordering values and identifying the middle value (or the average of the two middle values if there’s an even number of values).
- Identifying the mode as the most frequently occurring value in a dataset.
- Calculating the mean and median from frequency tables using appropriate methods.
- Estimating the mean and median from grouped data by using midpoints for classes and understanding the distribution of data.
- Comparing sets of data and their distributions using various averages.
|
Algebra Review
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding fundamental algebraic concepts and operations, including simplifying expressions, solving equations, and manipulating algebraic fractions.
- Knowing how to apply algebraic techniques to various types of problems, including linear and quadratic equations.
|
- Combining like terms and using distributive properties to simplify algebraic expressions.
- Solving linear and quadratic equations by isolating the variable and using methods like factoring or the quadratic formula.
- Simplifying algebraic fractions by cancelling common factors and performing operations such as addition, subtraction, multiplication, and division.
- Expanding and factorising algebraic expressions to solve equations and simplify problems.
- Applying algebraic methods to solve real-world problems and interpret solutions in context.
|
Transformations (not including enlargement)
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding basic types of transformations, including translation, reflection, and rotation.
- Knowing how each transformation affects the position and orientation of shapes on a coordinate grid.
|
- Translation: Moving shapes by a specified distance in a given direction using vector notation.
- Reflection: Reflecting shapes across a given line, such as the x-axis, y-axis, or a specified line of symmetry.
- Rotation: Rotating shapes around a point by a specified angle, such as 90°, 180°, or 270°, and identifying the centre of rotation.
- Using transformations to solve problems, including mapping shapes onto coordinate grids and interpreting the effects on their properties.
|
Venn Diagrams
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding Venn diagrams as a way to visually represent sets and the relationships between them, including union, intersection, and complement.
- Knowing how to use Venn diagrams to organise and analyse data, including two-set and three-set diagrams.
|
- Accurately drawing and labelling Venn diagrams to represent given sets and their relationships.
- Using Venn diagrams to find the union, intersection, and complement of sets.
- Solving problems involving sets by interpreting and analysing information presented in Venn diagrams.
- Applying Venn diagrams to solve real-world problems, such as finding probabilities or organising data.
|
Frequency Trees
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding frequency trees as a visual tool to represent the outcomes of events and how they split into categories or branches.
- Knowing how to use frequency trees to display and organise data from categorical events.
|
- Drawing and interpreting frequency trees based on given data or scenarios.
- Calculating the frequencies at each branch and using them to determine overall totals or probabilities.
- Using frequency trees to solve problems involving categorical data, including finding the frequency of specific outcomes.
- Applying frequency trees to analyse and interpret real-world situations and data distributions.
|
Englargement and similar shapes
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding enlargement as a transformation that changes the size of a shape while preserving its shape, based on a scale factor.
- Knowing that similar shapes are the same shape but different sizes, with corresponding angles equal and sides proportional.
- Understanding the concept of scale factor and its role in determining the size of an enlarged shape.
|
- Performing enlargements on shapes using a given scale factor and centre of enlargement.
- Identifying and proving that two shapes are similar by comparing corresponding angles and the ratios of corresponding sides.
- Calculating missing side lengths in similar shapes using the scale factor.
- Applying knowledge of enlargement and similarity to solve geometric problems, including those involving real-world contexts such as maps and models.
|
Trigonometry
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding the basic trigonometric ratios: sine, cosine, and tangent, which relate the angles and sides of right-angled triangles.
- Knowing the formulas:
sin(x) = opposite / hypotenuse
cos(x) = adjacent / hypotenuse
tan(x) = opposite / adjacent
- Recognising when to apply each trigonometric ratio based on the information given.
|
- Using sine, cosine, and tangent ratios to calculate unknown side lengths in right-angled triangles.
- Finding unknown angles in right-angled triangles using inverse trigonometric functions.
- Solving real-world problems involving right-angled triangles, such as determining heights, distances, and angles of elevation or depression.
- Applying trigonometry to solve geometric problems and interpret results in context.
|
Area and Volume Review
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding the formulas for calculating the area of various 2D shapes, including rectangles, triangles, parallelograms, and circles.
- Knowing the formulas for calculating the volume of 3D shapes, including cubes, cuboids, prisms, cylinders, and pyramids.
- Recognising the relationship between area and perimeter, as well as volume and surface area.
|
- Calculating the area of 2D shapes using appropriate formulas.
- Finding the volume of 3D shapes by applying the relevant formulas.
- Solving problems involving the area, perimeter, volume, and surface area in various contexts.
- Converting between different units of measurement when calculating area and volume.
- Applying area and volume concepts to real-world problems, such as finding the material needed to cover a surface or fill a space.
|
Fractions Review
| Unit Progress Criteria |
| Knowledge |
Skills |
- Understanding the basic concepts of fractions, including numerator, denominator, and equivalent fractions.
- Knowing how to convert between improper fractions and mixed numbers.
- Recognising how to perform operations with fractions and mixed numbers, including addition, subtraction, multiplication, and division.
- Understanding how to compare and order fractions.
|
- Simplifying fractions by finding the Highest Common Factor (HCF) of the numerator and denominator.
- Converting between improper fractions and mixed numbers.
- Adding and subtracting fractions with both like and unlike denominators.
- Multiplying and dividing fractions, including multiplying by whole numbers and dividing by fractions.
- Perform the four operations with mixed numbers.
- Comparing and ordering fractions by finding a common denominator or converting to decimals.
- Solving word problems involving fractions in various contexts, such as finding parts of a whole or sharing quantities.
|












